wintertreey 님의 블로그
2.4 연습문제, 프로그래밍 실습 본문
연습문제
1.
a= -2/3, b= 2
2.
a.
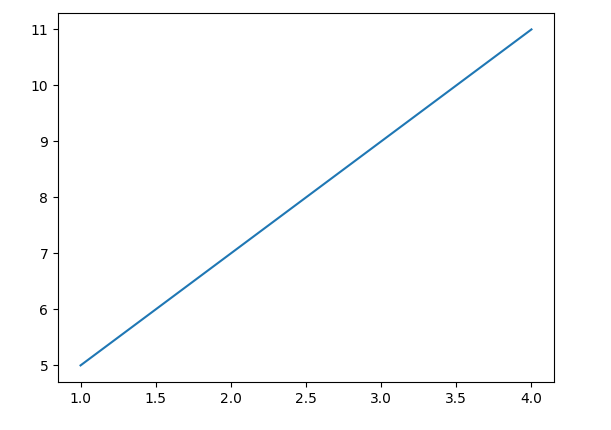
5 <= y <= 11
b.
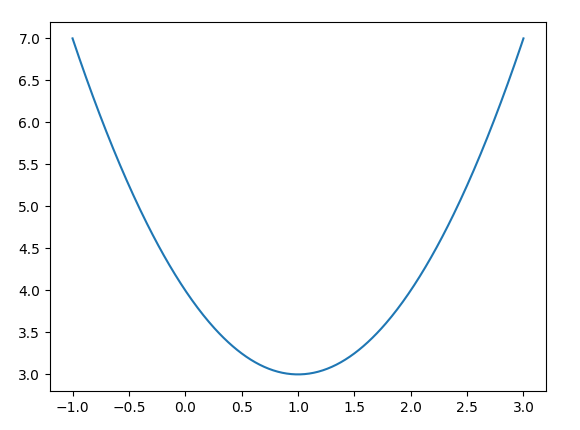
3 <= y
import numpy as np
import matplotlib.pyplot as plt
##x = np.linspace(1, 4, 301)
##y = 2*x + 3
##
##plt.plot(x, y)
##plt.show()
x = np.linspace(-1, 3, 401)
y2 = x**2 -2*x +4
plt.plot(x, y2)
plt.show()
3.
-13/4
4.
-6 < a < 2, 3
5.
a. -2^{4/3}
b. 10
6. 2^y = 16이라고 가정.
((1 - log_{3}{2} )) / 2log_{3}{2}
7. 3/4
8. ((2xy+1)) / ((2+xy))
9.

x = np.linspace(-2, 4, 601)
y = 0.5**(x+1) - 3
y_max = np.max(y)
y_min = np.min(y)
x_max = x[np.argmax(y)]
x_min = x[np.argmin(y)]
plt.plot(x, y)
# 그래프 상에 좌표 찍기
plt.scatter([x_max, x_min], [y_max, y_min],
color='red')
# 좌표값 텍스트 출
plt.text(x_max, y_max, f'({x_max:.2f}, {y_max:.2f})',
fontsize=9, color='black', ha='left', va='bottom')
plt.text(x_min, y_min, f'({x_min:.2f}, {y_min:.2f})',
fontsize=9, color='black', ha='left', va='top')
plt.show()10.

x = np.linspace(6, 12, 601)
log3_x = np.log(x) / np.log(3)
y = log3_x**2 - 4 * log3_x + 3
y_min = np.min(y)
x_min = x[np.argmin(y)]
plt.plot(x, y)
# 그래프 상에 좌표 찍기
plt.scatter([x_min], [y_min],
color='red')
# 좌표값 텍스트 출
plt.text(x_min, y_min, f'({x_min:.2f}, {y_min:.2f})',
fontsize=9, color='black', ha='left', va='top')
plt.show()해당 함수는 무한대이므로 최대값이 존재하지 않는다.
11.
a. x =1
b. x = 1
12.
a. x > -1
b. -3 < x < 1/3
13.
9/4
14. 6
15.
2, 3

x = np.linspace(-np.pi, 2*np.pi, 500)
y1 = 2*np.cos(x) + 4
y2 = -np.sin(4*x) + 7
y3 = 4*np.tan(2*x)
y4 = 5*np.cos(0.25*x) - 2
g1, = plt.plot(x, y1, label = '2cos(x)+4')
g2, = plt.plot(x, y2, label = '-sin(4x)+7')
g3, = plt.plot(x, y3, label = '4tan(2x)')
g4, = plt.plot(x, y4, label = '5cos(0.25x)-2')
plt.axhline(0, color='gray', linewidth=0.5) # x축
plt.axvline(0, color='gray', linewidth=0.5) # y축
plt.ylim(-20, 20) # tan그래프로 인해 y축 범위 설정
plt.legend()
plt.show()16.
패스
17. π / 4
18. π / 3. 2π / 3
19.
a. 2 π / 3
b. 3 π /4
20.
a. [ 0, π / 6 ], [ 11π/ 6, 2 π ]
b. [0, π /4], [ π , 5 π /4]
프로그래밍 실습
프로그래밍으로 그래프를 그려보는것도 의의가 있겠지만, 테일러 정리라는게 뭔지 좀 더 확인해보자.
테일러 정의란 간략하게 어떤 함수 f((x))를 일정한 점 근처에서 다항식의 무한급수로 근사하는 방법이다.
아주 유용한 개념이고, 특히 복잡한 함수의 근사 계산, 해석, 미분 방정식 해법 등에서 많이 쓰임.
'수학' 카테고리의 다른 글
| 3.2. 수열의 극한 (0) | 2025.07.08 |
|---|---|
| 3.1 수열과 점화식 (1) | 2025.07.02 |
| 2.3.3 역삼각함수 (1) | 2025.06.27 |
| 2.3.2 삼각함수 (0) | 2025.06.27 |
| 2.3.1 삼각비 (0) | 2025.06.20 |


