일차, 이차 방정식

다항함수

   단항식 3, 4x, 6x^2y, 3

   곱하기, 나누기로 연결.

 

   다항식 x+y+3, x^2+4y+7

   덧셈, 뺄셈으로 연결.

 

초월함수

   지수함수

   로그함수

   삼각함수

 

 

그래프 모양

                                                                      a > 0      우상향                                                      a < 0  우하향

 

 

 

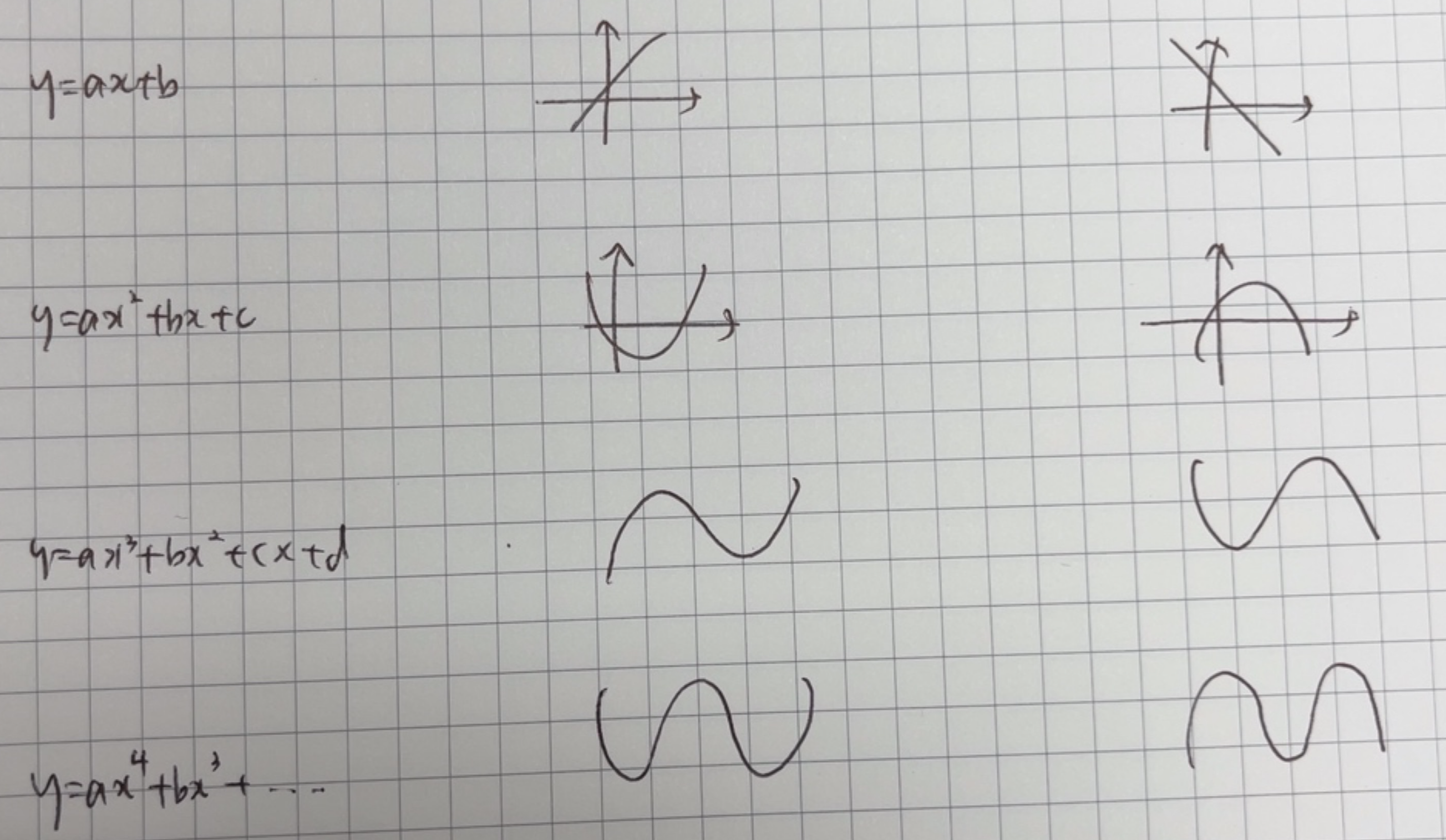
일차방정식

그래프의 교집합의 x 값 

 

 

 

           y절편

y= -3x + 6 

   기울기  

 

기울기

= y의 변화량 / x의 변화량. 절대값이 클수록 가파름.

 

그리는 법

1) 기울기값, 좌표 1 

2) 좌표 2

 

 

 

 

이차방정식

근의 공식

 

 

소인수분해

 

x^2 -3x -4 =0 <--전개---     (x-4)(x+1)=0

                       -인수분해->

 

 

근을 구하는 법

1) 그래프그리기

2) 인수분해

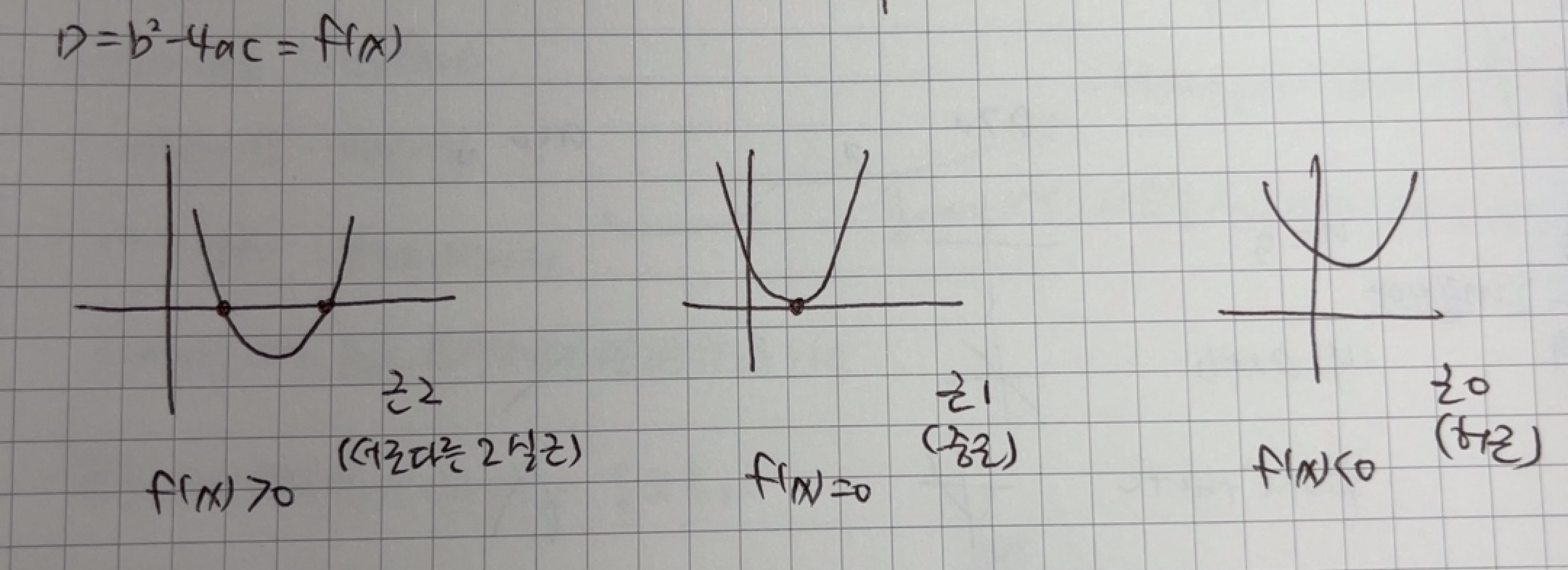
3) 판별식(D = b^2-4ac)로 근의 개수 판별

 

 

절댓값

= 원점부터의 거리.

 

 

 

 

---

 

번외.

나이와 키로 이뤄진 데이터가 있다고 해보자. 둘의 상관관계를 그래프로 표현해보고자 한다.

임의의 함수 직선그래프가 있다고 가정. 

 

오차값을 구할때 제곱을 해주는 이유는 오차값의 차이를 더하다보면 음수와 양수가 서로 합해져 0이 될 수 있기 때문이다. 

그렇게 오차값을 줄이며 기울기가 0에 수렴하는 가장 적합한 학습모델을 구현할 가중치w를 구하는 것.