wintertreey 님의 블로그
4.2 미분법 본문
http://www.kocw.net/home/cview.do?lid=a873e83b5fa99d33
AI를 위한 기초수학
이 강좌에서는 대학에서 다루는 미분적분학 관련 교과목을 전공하는데 필요한 기초적인 수학적 지식과 그 응용에 대해 알아본다. 특히 AI수학, 미분적분학과벡터해석(1), 미분적분학과벡터해석(
www.kocw.net
1. 미분법 기본 공식
미분 가능한 두 함수 f((x)), g((x))에 대해서 다음이 성립한다.
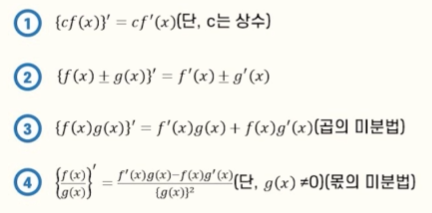
예제 4-5
a. f'((x)) = 2020x^{2019} + 9x^{2}
b. g'((x)) = $ \frac{1}{(x+1)^{2}} $
2. 삼각함수의 도함수
덧셈정리

예제 4-6
(4루트3 - 루트7) / 12
삼각함수의 극한
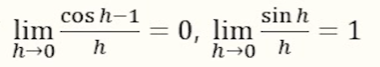
삼각함수의 도함수

예제 4-7
a. 2/3 b. 1
예제 4-8
a. cos^{2}x - sin^{2}x
b. 2xtanx + x^{2}sec^{2}x
3. 지수함수와 로그함수의 도함수
자연상수 e
$$ e = \displaystyle \lim_{x\to\infty }(1+\frac{1}{x})^{x} = \displaystyle \lim_{x\to0 }(1+x)^{\frac{1}{x}} $$
e 의 값은 약 2.719291...로 알려져 있다.
예제4-9
a. e^{3/2}
b. e

확인문제
1.
참



'수학' 카테고리의 다른 글
| 4.4 합성함수와 역함수의 미분법 (0) | 2025.08.28 |
|---|---|
| 4.3 고차도함수 (0) | 2025.08.28 |
| 4.1 미분계수와 도함수 (2) | 2025.08.25 |
| 3.5 연습문제, 프로그래밍 실습 (2) | 2025.08.23 |
| 3.4 함수의 연속 (0) | 2025.08.20 |


